ENZYME KINETICS

Introduction

The mechanism of an enzyme-catalyzed reaction is to determine the rate of the reaction and how it changes in response to changes in experimental parameters, a discipline known as enzyme kinetics. This is the oldest approach to understanding enzyme mechanisms and remains the most important.

TURNOVER NUMBER–Turnover number of an enzyme is the number of substrate molecules converted into a product by an active enzyme molecule per second when the enzyme is fully saturated with the substrate. Turnover is equal to the kinetic constant (in this case it is K2), also called k_cat. The maximal rate “V_max” reveals the turnover number of an enzyme if the concentrations of the active sites of an enzyme are known, then it will be written as- V_max=K₂[E]_T

Therefore, it can be written as, K₂=Vmax/[E]_T

The turnover numbers of most of the enzymes with their physiological substrates fall in the range of 1-10⁴ per second.

Enzyme	Turnover numbers (per second)
Carbonic anhydrase	600,000
3-Ketosteroid isomerase	280,000
Acetylcholinesterase	25,000
Penicillinase	2,0000
Lactate dehydrogenase	1,0000
Chymotrypsin	100
DNA polymerase 1	15
Tryptophan synthetase	2
Lysozyme	0.5

SUBSTRATE CONCENTRATION DEPENDS ON THE RATE OF ENZYME-CATALYZED REACTIONS

The key factor affecting the rate of the reaction catalyzed by an enzyme is the substrate concentration [S]. One simplified approach in studying Enzyme kinetics is to first measure the initial rate/initial velocity [V₀] when substrate concentration[S] is greater than enzyme[E]. But at low concentrations of [S], V₀ increases linearly with an increase of [S]. Whereas, at high concentrations, V₀ increases in smaller amounts as compared to [S] until a point comes where V₀ has its increment vanishingly small. This plateau-like region of V0 is close to the maximum velocity of V_max.

Here, V_max is extrapolated because V₀ does not reach V_max. The [S] where V₀ is half of its maximal, known as Km also known as Michaelis constant. Here, the ES complex is the key feature to understand the kinetics of the enzyme. Victor and Henri proposed in 1903 that the relationship between enzyme and substrate in the form of ES is a necessary step in enzymatic analysis. This idea was further explained in a form of an equation by Leonor Michaelis and Maud Menten in 1913.

• The enzyme first binds to the substrate in a fast reversible manner:
• The ES complex advances to a slower second step to yield a free enzyme and the product [P]:

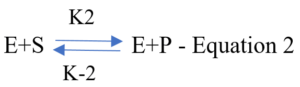
The slower second reaction is the rate-limiting step; therefore, the overall rate reaction is proportional to the concentration of enzyme-substrate complex [ES]. The maximum initial rate (Vmax) is observed theoretically when all the enzymes are present in ES and  where E is negligibly small.. Under these conditions, [E=ES], the enzyme is said to be saturated, that is, with an increase in the substrate concentration [S] the enzyme will not have any effect on the reaction. The saturation is the characteristic feature of enzyme catalysis and is observed as the plateau-like figure in Fig-1.

Steady state kinetics

The concept of steady-state was introduced by G. E Briggs and Haldane in 1925. When the enzyme is first added along with an excess of substrate, there is an initial short period called the pre-steady state. This reaction quickly reaches the steady-state in which [ES] remains approximately constant over time. The V₀ is measured by analyzing the steady-state even though it is limited to the early part of a reaction. This analysis is called steady-state kinetics.

The curve expressing the relationship between S and V₀ is the same for most of the enzymes and is expressed algebraically by the Michaelis-Menten equation.

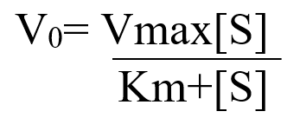
Now, we will introduce another term [Et] representing total enzyme concentration. The rates of formation and breakdown of ES are in detail explained by rate constants k1(formation) and k1+k2 (breakdown).

• Rate of ES formation = k1([Et-[ES]) [S] – Equation 3
• Rate of ES breakdown= k-1[ES]+k2[ES] – Equation 4

Dividing equation 1 and 2 and further simplifying, we get,

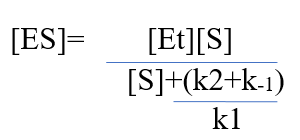The term (k2+k-1)/k1 is the Michaelis constant Km, therefore, it can further be simplified as,

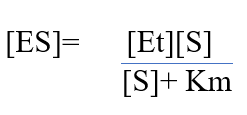Significance of K_m

• The Km can vary from enzyme to enzyme, and even for different substrates of the same enzyme.
• The term Km is an indicator of the affinity of an enzyme for its substrate.
• Higher is the value of K_m; lower is the affinity of the enzyme towards the substrate.
• Lower is the value of K_m; higher is the affinity of the enzyme towards the substrate.

Also, transforming the equation into a double reciprocal plot. First, taking the reciprocal of the Michaelis- Menten equation:

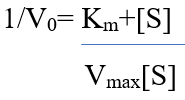Further simplifying the equation by separating the components,

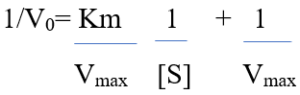
This form of equation is known as Lineweaver-Burk equation.

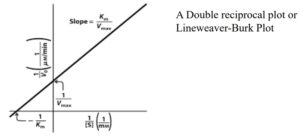
References and Sources:

• https://bionumbers.hms.harvard.edu/bionumber.aspx?id=105086&ver=1#:~:text=The
  turnover number of an enzyme, is the,from 1 to 10^4 per second (Table link).
• https://chem.libretexts.org/Bookshelves/Biological_Chemistry/Supplemental_Modules_(Biological_Chemistry)/Enzymes/Enzymatic_Kinetics/Michaelis-Menten_Kinetics
• https://alevelbiology.co.uk/notes/michaelis-menten-constant/
• https://bio.libretexts.org/Under_Construction/Cell_and_Molecular_Biology_(Bergtrom)/05:_Enzyme_Catalysis_and_Kinetics/5.04:_Enzyme_Kinetics
• https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7756376/
• https://faculty.ksu.edu.sa/sites/default/files/lab6_11.pdf
• https://www.inf.ed.ac.uk/teaching/courses/csb/CSB_lecture_enzyme_kinetics.pdf
• http://physics.bu.edu/~pankajm/PY571/Notes/Lecture4.pdf
• https://link.springer.com/chapter/10.1007/978-981-13-0785-0_15
• https://bio.libretexts.org/Courses/Wheaton_College_Massachusetts/Principles_of_Biochemistry/07:_Enzymes_catalysis_and_kinetics/7.02:_Derivation_of_Michaelis-Menten_equation

Also Read:

• Klebsiella: Introduction, Classification, Biochemical and Treatment
• Immunoglobulin: Introduction, Structure and function
• Whole-Genome Shotgun Sequencing: overview, steps and achievements
• ELISA- Principle, Types, Uses, Advantages and Disadvantages
• Delta Variant: Introduction, Transmission Rate, Symptoms and vaccination
• Bacterial Growth Curve: Definition, Phases and Measurement